Sciences et techniques dans l'art

Préambule : Ensemble de Mandelbrot en noir et blanc :


En fait l'ensemble des points de ce plan coloriés en noirs sont les valeurs du paramètre C du plan complexe  pour lesquelles la suite définit par
{Z0=0
Z(n+1)=(Zn)²+C} reste borné.

Définition des termes en gras pour comprendre :

Une suite:

Une suite 'récursive' est un ensemble de nombre ordonné définit de manière récursive, à partir d'un élément initial et d'une formule. On va noter le n-ième élément de la suite Z par Zn.

On définit donc une suite Z par son premier nombre Z0 et la formule qui permet de passer de l'élément 'n' à l'élément 'n+1'

Exemple de suite :
définition :
{Z0=0  <- élément initial
Z(n+1) = (Zn)² + 4    <- formule}

--------------------------

ainsi Z0=0 (par définition de la suite);

Z1=4
car Z1=Z0*Z0+4=0*0+4=4

Z2=20
car Z2=Z1*Z1+4=4*4+4=16+4=20

Z3 = 404
car...

La suite définit ci-dessus est l'ensemble ordonné : Z=  {0 ; 4 ; 20 ; 404 ; ...........}

la limite d'une suite
Une question que l'on peut se poser quand on définit une suite, c'est par exemple, quelle est la valeur qu'elle atteint quand n tend vers l'infinie.
Par exemple pour la suite Z définit plus haut, on constate que ses éléments Zn sont de plus en plus grands. On va tendre vers "+infini" quand n tends vers l'infini (dans ce cas, on dit que la suite diverge). il se peut que la suite reste dans un espace borné, ou mieux qu'elle convergevers une valeur particulière c'est a dire qu'au fur et a mesure des n, les valeurs de Zn se rapproche toujours d'une valeur particulière.

Troisième notions, ajout d'un paramètre
Si on reprends la suite Z ci-dessus :
{Z0=0
Z(n+1)=(Zn)²+4}

On peut s'amuser plutot qu'a mettre '4', a remplacer cela par un paramètre. Disons qu'on l'appel R.
Ainsi la suite se note Z_R et devient :
{Z0=0
Z(n+1)=(Zn)²+R}

On a donc une suite pour chaque valeur que peut prendre R, et on peut étudier la limite de la suite par rapport a se paramètre R.
En effet pour R=4 on a vu que la suite diverge, mais par exemple pour R=0, la suite Z converge vers 0.

Quand est-il pour R=0.0001 R=-1 ou R=0.12 par exemple ?

On peut démontrer que si R est compris entre -2 et 0.25 la suite Zn_R converge (pour chaque R vers une valeur différente bien sur) !

Représentation graphique en noir et blanc
Lorsque j'ai définit la suite Z_R, j'ai implicitement supposé que R était un paramètre a valeur dans l'ensemble des réels. (c'est a dire tout les nombres positifs ou négatifs que l'on peut écrire avec une  virgule et un développement décimale infinie)
Dans ce cas, le paramètre R peut se représenter sur une droite, la droite des réels :


et l'on peut colorier cette droite en noir épais si la suite Z_r converge, et ne rien faire sinon.

ça donne


Et disons qu'on appel Ensemble de Hamsterkiller, l'ensemble des point colorier en noir, c'est a dire l'ensemble des paramètre R, pour laquelle la suite définit par :
{Z0=0
Z(n+1)=Zn+R}
converge.


Le plan complexe:
On va dire que c'est la grosse marche et on va pas trop rentrer dans le détail, mais on va reprendre le modèle de notre suite Z_R sauf que cette fois, plutot que de contraindre le paramètre R a prendre des valeur dans les Réels, on lui permet de prendre des valeurs dans l'ensemble des nombre complexe. Ainsi on définit Z_C par :

{Z0=0
Z(n+1) = (Zn)²+C}

Cette suite a valeur dans les nombre complexe est exactement la suite qui permet de définir l'ensemble de Mendelbrot.

les nombre complexe Un nombre complexe se définit de la façon suivante :
C=a+b*i, ou a et b sont deux nombre réel et i, un nombre particulier définit par i*i=-1 (i est la solution de l'équation x²=-1), c'est a dire que i²=-1. On va dire grosso merdo que c'est sa seul particularité, les règles de calcul algébrique se passent pour le reste comme dans R.

Addition de deux nombres complexes : (3+5i) + (1-2i) = 3+1 + 5i - 2i = 4+3i
Multiplication de deux nombres complexes : (3+5i) * (1-2i) = (on distribue) : 3*1 + 3*(-2i) + 5i*1 + 5i*(-2i)
= 3-6i+5i - 10*(i)² = 3 -i +10 = 13-i


On peut représenter un nombre complexe, non pas sur une droite comme on le fait pour un nombre réel, mais sur un plan, le plan complexe :




Ainsi on a tout ce qu'il faut pour calculer les élément de la Zn_C définit par
Z0=0
Z(n+1)=(Zn)²+C

pour chaque C.

Pour les valeur de C pour laquelle la suite converge, on colorie le point du plan complexe en noir, c'est une représentation de l'ensemble de Mandelbrot.



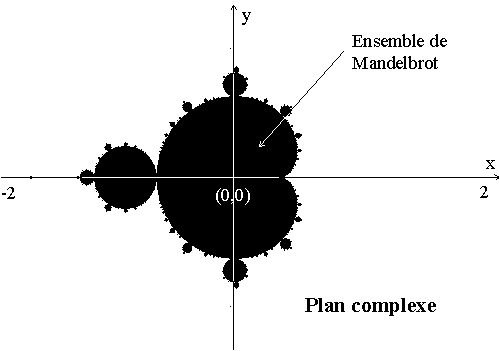
Il existe plein de façon de colorier autour de l'ensemble. Grosso modo plutot que de faire une coloration noir : converge ; Blanc diverge, on fait : Noir : converge  et on associe une couleur selon 'la vitesse' de divergence) et cela donne de bien belles images !